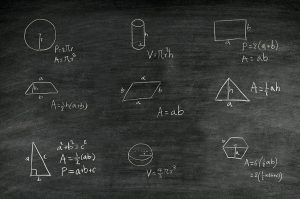Math Problems for 4th Graders

Entering the fourth grade can be very exciting, and comes with many challenges.  Student’s math skills will be kicked up a notch this year, as they are expected to have a firm foundation with basic operations and facts so that more complex structures and concepts can be introduced.  Practicing basic concepts first is essential, as they are the building blocks to be able to comprehend and utilize these new mathematical features.  Practicing the concepts for perfection and complete understanding can help 4th graders master these skills.

In this article, you will find information about each essential skill that a 4th grader should practice to mastery, including:

Angles

Lines, Line Segments, & Rays

Graphing skills become essential in the fourth grade, as is learning how to manipulate lines and angles to create polygons of multiple shapes and dimensions.  Beginning with lines and line segments, students learn how to measure, plot, and use lines and rays in more complex geometry.

Parallel, Perpendicular, Intersecting Lines

New mathematical vocabulary presents three different terms for line relationships – parallel, perpendicular, and intersecting lines.  As they work with these relationships, they will see the relationship between line patterns and the creation of angles.

Types of Angles

Acute, obtuse, and right are standard terminology for angles, but using them with actual shapes and in mathematical calculations increases higher order thinking.  Fourth graders will continue to process these angles’ relationships with objects in the real world.

Estimate Angles

Just as estimating money helps us calculate and budget, estimating angles can help us visualize spatial awareness and see angles in the real world.  One the three basic types are mastered, students will learn subdivisions of acute and obtuse and how to visualize their degree measure.

Area & Perimeter

Perimeter of Squares and Rectangles

Perimeter is simply the distance around objects, but mastering addition and calculating square and rectangular shapes is essential for a fourth grader.  Once they master the four sides, they can move onto calculating the perimeter of polygons and circles.

Area of Squares and Rectangles

Multiplication combined with length measures enables students to calculate the area of objects and spaces.  This is essential for tasks like placing furniture in the real world, or measurements for larger spaces.

Dates and Telling Time

Adding & Subtracting Mixed Time

Moving beyond basic hours and quarter hours, fourth graders begin to relate quantities of time to more complex calculations.  Understanding the concept of seconds, minutes, and hours helps students to master time-related problems.

Converting Units of Time

From seconds to minutes to hours, students should be able to know the relationship between units of time.  After they grasp this concept, calculating and converting units of time will become easy using their multiplication and division skills.

Portions of Time 

Larger than just minutes and hours, days and weeks and months are larger chunks of time that students will need to estimate.  “How long is an hour?”,  “How many days in a week?”,  and “How long will it take for time to pass?” are all concepts students will master.

Time Zones

Calendars

Plotting larger units of time on a calendar and understanding how a year, decade, and century work are prime skills for 4th graders.  Using calendars to plot and plan gives students real world skills for success in life.

Decimals

Decimal Place Values & Expressed in Words

Once kids learn what a decimal is, they will begin to understand the place value and how that translates into words.  The concept can be difficult at first, as it is in reverse order from what they used in whole numbers.

Equivalent Decimals, Fractions, & Rounding

Understanding the relationship between decimals and fractions can be a difficult concept, but visuals help to bridge the gap.  Then kids will understand when and how to round once they know which is more than or less than half and understand place value.

Comparing and Ordering Decimals (up to Hundredths)

Once place value understanding is solidified, kids will be able to order and compare decimals more accurately.  Number lines often help them to do this, as having a visual can help them to better manipulate the numbers.

Converting Fractions to Decimals & Mixed Numbers

This is a higher order skill once kids have mastered the basic fraction to decimal equivalency.  When you include whole numbers into the mix, kids must recognize the equivalency of both and have the skills to complete multiple steps.

Adding and Subtracting Decimals

While it might not seem like a difficult concept, many kids struggle with lining up the decimal when adding or subtracting.  The addition of zeros to the end in order to properly complete the operation is sometimes confusing, so practice helps.

Division

Division Sentences

While it might not seem like a tricky concept, some students struggle when you move from using this symbol ⟌ to division problems in a sentence with the ÷ symbol.  It can be hard to visualize and creates another step wherein kids must know mental math or be able to insert the numbers correctly into the ⟌ setup.

Inequalities with Division

Division can be used to reduce inequalities to a simpler form, but it is a new concept for some.  When you divide an inequality by a negative number, you must flip the inequality symbol.

Divide by One-Digit Numbers (within 100)

Simple division facts are foundational.  When students master multiplication, this becomes very easy to relate the difference between the two.  However, if multiplication facts are lacking, division will be very difficult.

Properties of Division

There are properties that rule division that students must master, including dividing by 1, by 0, and by itself.  Students will learn these concepts early before moving into complex division work.

Fractions

Equivalent Fractions Using Models

4th graders do really well when they have visuals to compare new concepts to, and using models helps this process.  Something as simple as a pie chart evenly divided can show kids how to picture equivalent fractions.

Comparing & Ordering Fractions

When beginning to compare fractions, kids will first learn the benchmark fractions that are most commonly used – think about those used in baking cups.  Then they will be more adept at being able to say which are equivalent and begin to learn how to reduce them properly.

Decompose Fractions

Breaking down fractions into units can help kids understand equivalencies and to see how the units compose a whole. This will help them to construct number sentences with a series of smaller fractions that add up into one larger fraction. 

Add, Subtract, & Multiply Fractions

Unit fractions – fractions with a numerator of 1 – are what most kids begin learning, plotting them on a number line to see how they relate.  Eventually they will learn to add and subtract fractions with a common denominator and then to multiply by whole numbers.

Mixed Numbers & Proper/Improper Fractions

Once the basics of fractions have been mastered, students are prepared to manipulate mixed numbers and both proper and improper fractions.  These problems will require multiple steps to solve a single problem, involving multiple operations.

Geometry (Shapes)

Shapes & Polygons

Identifying basic shapes should be second nature to 4th graders, but more complex shapes will arrive this year.  In addition, using a variety of math skills, including perimeter and area formulas, will be practiced.

Lines & Angles

Line segments, parallel lines, and perpendicular lines will all be presented.  Once two lines intersect or bisect, students will learn about a variety of angles.

Triangles

Triangles have a variety of properties that students will learn this year, including specific terminology such as hypotenuse.  Formulas for area and working with right angles require mastery through practice.

Lines of Symmetry

Visualizing lines of symmetry and being able to draw them on shapes teach students the concept of ½  and mirror images.  Practicing with a variety of shapes, both 2D and 3D, will help them to see symmetrical items in everyday objects.

Circles

2D circles require even more complex understanding in order to use the formulas for perimeter and area.  Students will learn how to use a radius and diameter measurement as well as the value of pi.

Classifying Shapes by Angles and Sides

An easy way to identify shapes is by the number of both angles and sides.  Some are very specific, including squares and rectangles with four 90-degree angles, while larger shapes will have more shapes and angles.

Reflection, Rotation, and Translation

Visualizing shapes in both 2D and 3D forms will help students to decipher which formulas and which measurements to use to solve problems.  Studying how shapes reflect and rotate can help students visualize complementary shapes in the real world.

Linear Functions

Input/Output Tables

Tables that show the relationship between sets of numbers that follow the same rules.  The can be both simple with only one operation involved, or complex, with multiple operations required.

Function Tables

A function table allows students to describe a function using the relationship between inputs and outputs.  There is always one rule that is followed for each table.

Generating Patterns and Graphing Relationship

When using numerical rules, students will see that each creates a different numerical sequence.  You can often compare two sequences by graphing them to see their similarities and related rules.

Mixed Operations

Input/Output Tables

Learning how to not only insert numbers into a formula to create an output scenario, but also extracting the data for plotting are both essential skills.  Finally, creating a table or graphing the results completes this skill set.

Order of Operations

How to approach problems with multiple operations required isn’t as difficult as it sounds once students master PEMDAS – an acronym that tells them in what order to complete the problem.  Parentheses, exponents, multiplication, division, addition, and then subtraction is the name of the game.

Money

Adding Money & Making Change

Using money is an essential life skill for every person, and we can’t always depend on the cash register.  Adding the price of items together not only firms the foundation for budgeting, but it also enables 4th graders to practice decimals in a real-world setting.

Price Lists & Unit Price

Translating costs of items to a receipt format can often be confusing for kids at first.  But manipulating decimals and incorporating complex math with multiplication to price units and addition with decimals preps the average 4th grader for the real world.

Rounding Money Amounts

For quick mental math, using a real-world application like rounding money will help kids learn to estimate in their head.  This makes calculating overall cost and budgeting on the go becomes second nature.

Multiplication

Inequalities with Multiplication

Once 4th graders have secured basic multiplication facts, they can begin multiplying numbers of multiple digits.  Comparing two straightforward numbers isn’t difficult, but when you get more complex with mixed numbers or improper fractions, multiplication is required to find common denominators and eventually the solution.

Order of Operations

Learning the order in which to solve a more complex problem can be difficult without the acronym PEMDAS.  This simple word helps students solve equations by remember the proper order:  parentheses, exponents, multiplication, division, addition, and subtraction.

Ordering Numbers

Compare Numbers Up to Billions

The older students get, the more they are able to understand the meaning of larger quantities.  Place value helps them learn the name, but paying attention to exactly how many smaller components it takes to make the larger number takes higher order skills.

Inequalities Involving Multiplication and Division

Comparing numbers is a huge theme this year, especially understanding the greater-than and less-than signs.  Often students will have to solve both sides of an equation before they can compare numbers.

Place Value

Place Value Models Up to Ten Thousands

Unit blocks can help students to practice their understanding of place value.  Blocks of ten are often grouped to help students really understand the concept of values up to ten thousand.

Convert Between Place Values

Understanding basic relationships in terms of place value helps students understand a variety of concepts.  Beginning with the idea that 1 ten = 10 ones, students will work with a variety of numbers in varying sizes to further understand relationships.

Probability & Statistics

Calculating Probability

Probability can be calculated by determining a single event with one outcome.  The total number of outcomes that can occur is next.  Finally, dividing the number of events by the number of possible outcomes will help students to calculate the probability of an event.

Mean, Median, Range, & Mode

Learning the definitions of each term as well as how and when to use them will help students with real world issues, such as meteorology.  Mean is the average, while median is the middle number, range is the smallest to the largest number, and mode is the value that appears the most often in a series.

Units of Measurement

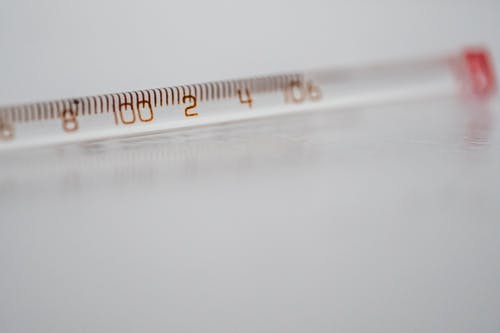
Temperature

While old-fashioned thermometers aren’t used much any more, students should still know how to properly read a thermometer.  The relationship between the seasons and the temperature will also be explored.

Whole Numbers

Understanding what makes up a whole number will help students with the higher order thinking skills required to complete more complex number sentences.  In addition, it also helps them to function in the real world before learning the details.

This list can be awfully overwhelming when you read it for the first time, but don’t forget these skills are to be learned throughout the entire school year.  Practicing skills repetitively helps to solidify it into their memory